Egy újabb érdekes elméleti témát boncolgatok: a bütyökgeometria, a szelepmű kialakítás és ezek hatása a motor tulajdonságaira.
A legegyszerűbbnek azt látom, ha belevágok a közepébe és illusztrációkon keresztül elemezgetem ki a képpel bemutatni kívánt problémákat.

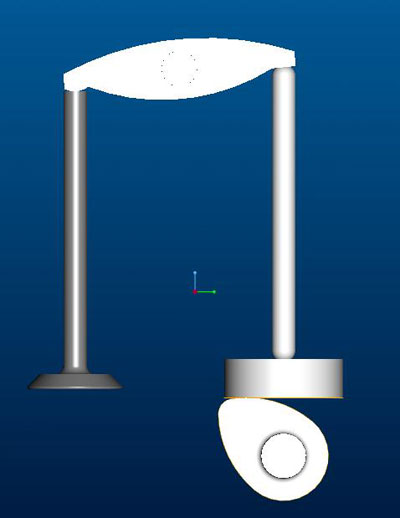
A fenti képen egy a teljesség igénye nélkül összeállított szimbolikus szelepvezérlés-részlet van. Amit a képen érdemes megfigyelni, hogy a bütyök ahogy végigfut a hidrotőke felületén, nem mindig a lökőrudak hatásvonalában ér hozzá a felülethez: hol jobbra, hol balra lökdösi azt. Ez a lökőrúd és a bütyök-hidrotőke érintkezési pontja közti távolság miatt forgatónyomatékkal hat a tőkét vezető felületre, ami erős oldalirányú erőket, és ezáltal erős koptató igénybevételt jelent. Ahogy a bütyök működő felülete végigfut a tőkén, folyamatosan vándorol a jobb és a bal oldala között.

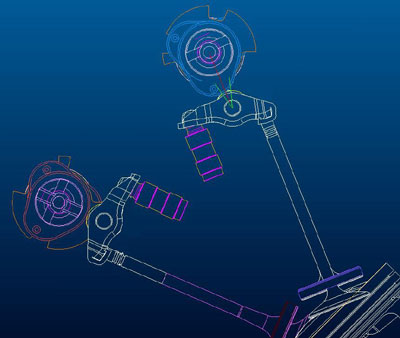
Ezen a képrészleten egy hengerenkénti négyszelepes (külön szívó-, és külön kipufogóoldali vezérműtengellyel) V-motor kis részlete látható. Ami érdekes az egészben, hogy a hidrotőke áll, és a himba közepére hat a bütyök. Előnye, hogy a nagyon kicsik mozgó tömegek, ami miatt jóval kisebb rugóerőket kíván a szelep, így a szelepek tömegét is csökkenteni lehet (nem fog leszakadni a szeleptányér a szelepszárról), kisebb szilárdság is elegendő. A kisebb szelepszár vastagság (6mm) kisebb tömeget jelent és nem elhanyagolható, hogy kisebb áramlási ellenállást is. További előnye azáltal, hogy a hidrotőke nem mozog, hogy a nyomás alatti olaj állandóan ott áll "készenlétben" a hidrotőke pufferterében és ha a nagynyomású térben olajveszteség lép fel, azonnal tudja pótolni. A CVH motorban a tőke mozgása miatt, amíg mozog a tőke, le van zárva a furat, így jelentősen kevesebb ideig van lehetőség pótolni a tőkékből elszivárgott olajat.

Hátránya viszont a nagyon nehézkesen kialakítható bütyökprofil, ugyanis míg a bütyök legördül a himbába épített görgő felületén, változik az erőkar, amin keresztül a szelepet mozgatja. Az ábra jobb oldalán lévő bütyöknél, a himbában lévő görgő középpontjából indul két zöld rövid vonal. Ezek a vonalak, ahol metszik a görgő felületét, azok a pontok jelölik a nagyjából azt a két véghelyzetet, ahol a bütyök hozzáérhet a görgőhöz. A himba teljes erőkarja (tőkétől a szelepszárig) ~40mm. A bütyök nagyjából a közepén nyomja a himbát (~20mm-re a tőkétől), de a görgőn való legördülés miatt ~pluszmínusz 3-4mm-t mozog a bütyök hatásvonala. Számszerűen 16 és 24mm között. Vagyis a 40/16-os erőkar aránya 2.5, míg a 40/24-é csak 1.6. Ez azt jelenti, hogy ha nagyobb az erőkar, akkor a bütyök azonos emelése ellenére a szelepemelésnél már 56% eltérés jelentkezik. Számszerűen: vegyük azt a pontot, ahol a bütyök 3mm-t emel; ha a baloldali zöld vonalnál teszi azt, akkor a szelepnyitás 3mm x 40/16 = 7.5mm; Ha a jobb oldali zöld vonalnál teszi, akkor 3mm x 40/24 = 5mm lesz a szelepek nyitása. Konklúzió: egyforma karakterisztikájú szelepnyitáshoz és szelepzáráshoz teljesen másmilyen fel-, és lefutási oldalú bütyökre van szükség. Valamint erősen belekalkulálandó a karakterisztikába, hogy ha a bütyök a vezérműtengelyen az óramutató járásával ellentétes irányban forog, akkor a nyitáskor a nagyobb áttételű erőkar miatt a szelep gyorsabban fog nyitni és a kisebb áttételű erőkar miatt lassabban fog zárni. Fordított irányú forgásnál ez pont fordítva fog történni.

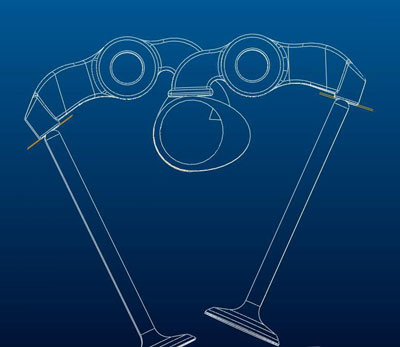
A fenti képen egy egy-vezérműtengelyes, négyszelepes motor szelepvezérlés részlete látható. Ennek a konstrukciónak az óriási előnye az alacsony beépítési magassága. Hátránya viszont a szelephézag manuális állítása, mivel hidrotőke beépítésével már jelentősen megnőne a beépítési magasság. Viszont az erőkar változása miatti - fentebb részletezett - problémák itt is jelen vannak, nem is kis mértékben. Ahhoz, hogy ezt kompenzálni lehessen, jóval nagyobbnak kellene lennie a himba forgástengelye és a vezérmű tengelye közti távolságnak, mint a másik oldal erőkarjának. Viszont így a bütyök emelése is nagyobb kell, hogy legyen, mint a számunkra szükséges szelepemelés mértéke, így viszont nőnek a méretek is... Vagy pedig marad a nagyon eltorzult, aszimmetrikus geometriájú bütykök.

És most egy kicsit a bütykökről. Bármennyire is olyan egyszerűnek tűnik, mint egy 100-as szög, azért egy "picit" összetettebb a kérdés. Egyes (egyetemi) tankönyvekben még említést tesznek a 3 ívből összeálló bütyökről, de szerintem már nagyon-nagyon sok éve nem létezik ilyen új konstrukcióban. Ennek nagy előnye, hogy egy körzővel és az emelés belekalkulálásával körülbelül 38mp alatt megrajzolható a beméretezett bütyök. Aztán azon túl, hogy "végül is ez is működik", más jót nem is lehet mondani róla. Zajos, iszonyatos erőkkel terheli a vezérmű-részeket és ezáltal több nagyságrenddel nagyobb kopást idéz elő, mint a többi geometria. Ez így néz ki:

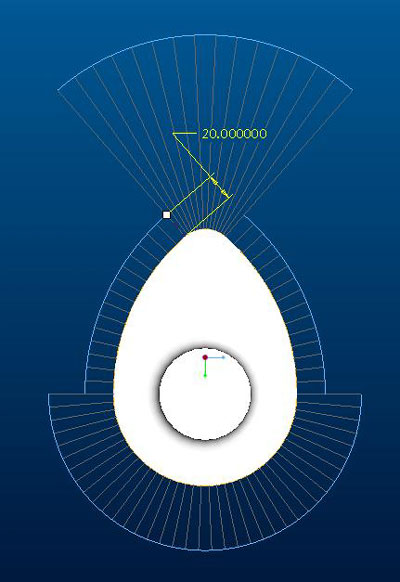
A bütyök kontúrja felett az ív görbülete (a görbület = a rádiusz reciproka, vagyis G=1/R) rajzolódik ki. Mielőtt elemezgetni kezdeném a bütyök hatásait, egy kicsit címszavakban a foronómiai görbékről. Foronómiai görbéknek egy mozgás jellemző görbéit nevezzünk, legtöbbször egy diagramban ábrázolva. Ezek közé tartozik az út (ebben az esetben a szelepemelés), a sebesség és a gyorsulás. A szeleprészek elemzésébe bele szokták még venni az erőfüggvényt is.

Az alábbi jelöléseket felhasználva:
s: út (szelepemelés)
v: sebesség (szelep pillanatnyi sebessége)
a: gyorsulás (szelep pillanatnyi gyorsulása)
F: erő a bütyök és a hozzá csatlakozó elem között (hidrotőke, lökőrúd, himbagörgő, stb.)
K: konstans

És még egy kiegészítés: a gyorsulás lehet pozitív is és negatív is. Csak a negatív gyorsulást a konyhanyelv lassulásnak nevezi.
Az út, a sebesség és a gyorsulás függvényei között az integrálás és a deriválás teremt kapcsolatot, de mivel nem kívánok magasabb szintű matematikába bonyolódni, így egy egyszerű példával próbálom magyarázni:

• ha egyenletesen haladunk, akkor a gyorsulásunk nulla, a sebességünk állandó és az általunk megtett út lineárisan növekszik. Tehát az a = 0 kifejezésen nincs mit magyarázni. A sebesség konstans, tehát a nulladik hatványon van, így a függvénye egy diagramban, ahol a vízszintes tengelyen az idő fut, egy vízszintes vonal lesz. Az út függvénye lineáris lesz, egy jobbra-felfelé mutató, szögben álló egyenes. Vagyis a gyorsulás nulla, a sebesség nulladfokú, az út pedig elsőfokú lesz.
• ha viszont egyenletesen gyorsulunk, akkor a gyorsulás konstans, vagyis nulladfokú lesz, így a diagramban egy vízszintes egyenes lesz belőle. A sebesség lineáris, vagyis elsőfokú, így a diagramban egy ferde egyenes lesz belőle, az út pedig másodfokú lesz, tehát a diagramban parabolikus jellege lesz a görbéjének.
• és ebből már logikusan következik, hogy ha a gyorsulásunk sem állandó, hanem mondjuk lineárisan nő, akkor a sebességfüggvényünk már másodfokú lesz, és az útfüggvény már harmadfokú.

Amennyiben adott a gyorsulásnak egy összetettebb függvénnyel megadott alakja, akkor abból már csak integrálással számítható a valós sebesség és út függvény.

Összegezve, egyszerű függvénnyel leírható mozgások esetén az út mindig egy hatvánnyal magasabb kitevőn van, mint a sebesség, és kettővel magasabban, mint a gyorsulás. Ebből következik, hogy a sebesség egy kitevővel van magasabban, mint a gyorsulás. És mindezt miért mondtam el? Tehát visszatérve a fenti ábrához, az ívek találkozásánál a görbület értékében ugrás jelenik meg. Ezt lehetne "függőleges eseményként" nevezni, ami annyit tesz, hogy nulla idő alatt kell valaminek egy adott szintről egy másik szintre ugrania. Ezt még az elektronikában is meglehetősen nehéz megvalósítani, ott is idő kell - csak jóval kevesebb - értékugrások létrehozásához, de a mechanikus részek esetében ez még sokkal lassabban megy csak. És a konkrét példánál maradva képzeljük el azt a pár pillanatot, amikor a szelepszár - a közvetett részekkel együtt - a bütyök alapkörén csúszik és várja a nyitás pillanatát. Amíg az alapkörön van, addig egy helyben áll, nem történik semmi. Viszont amint elér az alapkör és a felfutó ív találkozásához, ott egy gondolatvillanás alatt már v sebességgel kell nyílnia a szelepeknek. Ha ezt képletszerűen próbáljuk felírni, akkor a v=a*t összefüggést felhasználva látszik, hogy ha az idő (t) értéke a nullához közelít, akkor a gyorsulás (a) értéke erősen kezd a végtelen irányába elszállni. A nagy értékű gyorsulások végett a felfutó-ágban óriási erők lépnek fel, a bütyök tetején a szeleprészek elválhatnak a bütyöktől, a lefutó-ágban pedig az iménti elválás miatt pattoghat lefelé végig a szelep a bütykön. Szélső esetben a bütyök tetején ahogy elvált a szelep a profiltól, a lefutó-ágban már csak a bütyök kontúrja felett lobogva próbál visszatérni a helyére, majd találkozva a szelepfészekkel, csattan egy szépet nagyot és még vissza-visszapattan egyszer-kétszer, mire végre megáll. Természetesen ez a probléma nem csak ennél a bütyökprofilnál jöhet elő, elgyengült vagy alulméretezett szeleprugók esetén bármikor, de ennél különösképp jó esély van rá.

És ha ezt gyorsulás-problémát az erők irányából közelítjük meg, F=m*a összefüggésből látszik, hogy végtelenhez tartó gyorsulás ugyanilyen mértékű erőt is hoz létre. Ezeket a végtelenbe tartó erőket ugyan az anyag rugalmassága valamelyest tompítja, de ez a periodikus igénybevétel fárasztó igénybevételként jelentkezik, ami előbb-utóbb valamelyik alkatrész törésével végződhet.

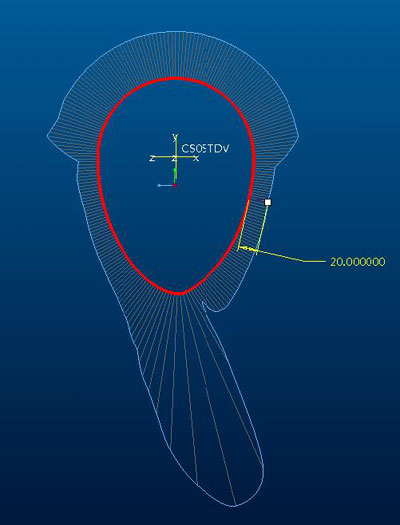
Ezen a ábrán azzal az első képen látható kezdetleges OHV vezérléssel kísérletezgettem, milyen bütyökprofilra van szükség ahhoz, hogy a szelepek szinuszosan mozogjanak. Természetesen a töltetcsere szempontjából az ideális az lenne, ha nulla szelepnyitási és szelepzárási időkkel lehetne számolni és közöttük pedig végig maximális lökettel lennének nyitva a szelepek. De ez nem valósítható meg, és a mechanikus igénybevételek miatt szép "lágy" mozgást kell megvalósítani, aminek mondjuk egy szinuszos mozgás meg is felel. Az én legnagyobb meglepetésemre (is) ez nem szimmetrikus bütyökprofilt feltételez. Ennek a bütyöknek a görbületén jól látszik, hogy a görbületi vonal mindenhol folytonos, csak nem mindenhol érintőleges. Ez a bütyökprofil már másodrendben is érintőleges, mivel a rádiuszok értékének a változásában nincs ugrás, teljesen folytonos. Ezzel gyakorlatilag már teljesen ki vannak küszöbölve a "függőleges események", így nincsenek túlterhelve mechanikusan a vezérműrészek.

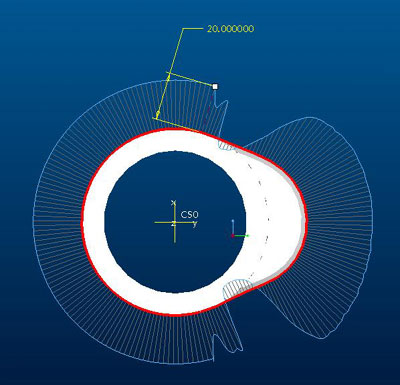
Ezen a képen egy homorú fel- és lefutási oldalú bütyök látható. Ezt onnan lehet tudni, hogy a görbület átmegy negatív tartományba is. Ennek a görbének az óriási hátránya, hogy csak görgős szelepemelővel használható, hiszen ha egy homorú bütyöknek kellene egy sík felületen végigcsúsznia, akkor a homorú részek között nem futna végig minden ponton, volna egy olyan szögállás, amikor a szelepemelő egyszerre két, egymástól több mm-re lévő ponton egyszerre feküdne fel, s így a két pont között egy jelentős részt átugrana. És a homorú felület átugrását követően a másik ponton folytatná az emelést, ami olyan extrém gyorsulást hozna létre, ami miatt talán egy-két órás járás után biztos, hogy valami törne. Tehát homorú bütyök csak görgős emelővel! A miértjére választ lehet kapni egy kicsit elemezgetve a második képet. És ami viszont óriási előnye ennek a bütyöknek, hogy egy lágy, de gyors felfutás után a lehető legjobban van nyitva, majd egy lágy lefutással fut le. Eredménye a csendes járás és a nagy nyitás miatt többlet-teljesítmény a hagyományos bütykökhöz képest.

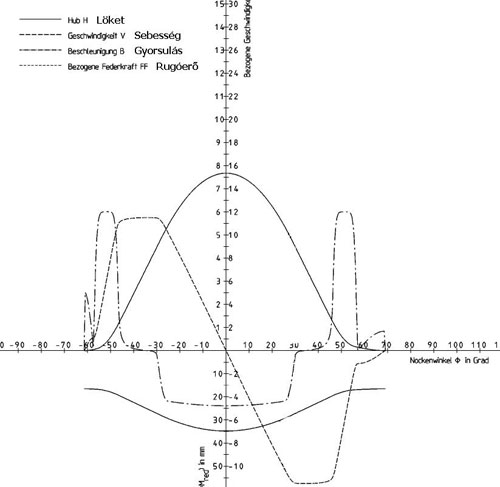
Ez a kép a fenti bütyök által megvalósított mozgásjellemzőket ábrázolja. A közel szinuszos folyamatos vonal a szelepnyitás görbéje. A diagram tengelymetszetén átmenő szaggatott vonal a szelep sebesség-görbéjét, míg a pontvonal a szelep gyorsulásgörbéjét ábrázolja. A vízszintes tengely alatt a rugóerő látszik. Amit érdemes kielemezgetni egy kicsit, az a gyorsulásgörbe. Látható, hogy a szelep nyitásakor és a szelep zárásakor lép fel a legnagyobb gyorsulás. A szelep nyitásakor azért, mert az álló szelepet kell viszonylag rövid idő alatt mozgásra kényszeríteni, és ha a szeleprészek között akár csak 0.2mm hézag is van (ez nem azonos a beállítandó szelephézag értékével, ez az üzemi körülmények között megmaradó hézag), akkor 7000-es percenkénti fordulatnál simán felléphet egy impulzusszerű 30000G-s (!!!) gyorsulás. (Számszerűen: 5 ezred másodperc alatt nulláról több, mint 500km/h!!!) (Vagy úgy kézzel foghatóbb, hogy 0.1mp alatt nulláról 10800km/h...?!?) :-D Mondanom sem kell, hogy ezt azért nem sok minden bírja ki. Ez persze elméleti görbe, és ez a gyorsulásérték még talán ezredmásodpercekig sem tart, s a valóságos anyagoknak van rugalmasságuk is, tompítják ezt, de túl csúnyák az eredeti értékek ahhoz, hogy ebből egy megnyugtató értéket kaphassunk. És körülbelül ilyen gyorsulásértékekről beszélhetünk akkor is, ha homorú bütyköt használunk görgős emelő nélkül. A szelepzáráskor pedig azért van nagy gyorsulás, mert a szelep közel egyenletes sebességgel zár és közelít a szelepülékhez, majd hirtelen kell megállnia, amit egyrészt a bütyök vége próbál lassítani, amit pedig nem sikerül, az csattan, majd pattog a szelepüléken.

Nos, eme rövid kis elméleti bevezető után egy kicsit át lehet értékelni a szelepvezérlés és bütykök kialakításának az egyszerűségéről gondoltakat...

bevezetés

1

2

3

4

5

6

7

8